Manual Fractal Art by meredithian
May 21st, 2008 9:31 AMManual Fractals - this time with Legos!
NOTE: For the sake of easy reading, the MATH! is in the footnotes.
When I saw this task my first thoughts ran immediately to a 3D construction with Legos. I thought it would be possible and possibly not very difficult to build a fractal out of Legos. After all, a fractal is simply a geometric shape that is self-similar and constructed recursively1.
The most basic fractal can be constructed with lines. Given a line of a certain length, say from 0 to 1 on the real line, copy this line below the original line, but divide the line into three segments and remove the middle portion. Divide each of the remaining two segments into thirds, remove the middle section, and copy the lines below. Repeat until you are down to dots and cannot split things any further.
This is called a Cantor ternary set2. Here's an example of what it should look like:

Since the lines are proportionally similar to one another, and the topmost lines can be said to be made up of the smaller lines, it is self-similar. And it is constructed recursively by using the process in step two on the results of the process from step one, and so on. It's not very interesting to look at, but a simple example of how fractals can be constructed.
There are lots of different kinds of fractals but for the purpose of constructing one from Legos, I thought the Menger Sponge would be perfect. While not as eye-catching as some sets, it is square, easy to mentally calculate and visualize, and its boxy nature would lend itself perfectly to my building materials.
FRACTAL 1: The Menger Sponge
Attempt 1
The plan I had was to use as many of these

as I owned or could obtain, and stack them into cubes of 9 x 9 x 9, then remove the necessary pieces to create the first iteration of the sponge. Then, I would make 20 of those cubes3 to build a larger cube for the second iteration. The whole thing, I imagined, would be about a cubic foot or less – about the size of a breadbox. Totally manageable! Then if I got more Legos, like a LOT more, perhaps through collaborating with other FØEcakes, I hoped I could expand to a third iteration and that would be quite big enough; really as far as I would ever want to go.
This was, of course, a total pipe dream. For starters, while one iteration would only take 20 2x2 bricks, which seemed reasonable and doable, two iterations would take 400! I have a lot of Legos, but I knew I had little hope of making it that far.
Another reality I discovered that stood in my way is that Legos, individually, are quite expensive. Looking at the Lego website4, to get one hundred 2x2 bricks, it would cost me $110! Obviously ordering several hundreds of them was beyond reason.
I immediately put out a call to all FØEcakes for Legos, and though I was directed to a reliable Legomaniac resource, and still had doubts about getting that many 2x2 bricks. But before I could despair much over that problem, I realized another, more critical flaw in my plan:
 .
.Menger sponge attempt 2
After figuring out a way to make this thing stay together (though I had to eliminate the idea of using all 2x2 bricks which made it not totally self-symmetric) I created this

but it was obviously, well, not a square.
Although outward symmetry wasn't as important as self-symmetry I longed for it anyway.
Menger sponge attempt 3
I decided I could perhaps construct a more fully square square, of many different kinds of pieces (hopefully cutting down in my need for many, many square bricks) and that would be my smallest unit. This also, turned out to be somewhat impractical. I tried a lot of stuff, but this was the first thing that worked used this square constructed of smaller 2x2 and 2x4 bricks:

It was not ideal, but I attempted to build the sponge again anyway.

This is indeed a fractal folks, just a really clunky ugly one.
This monster used a lot of pieces, though, and I was running out of pieces, fast. I would never be able to spell out FØES - or even just Ø - with the rate I was using pieces. I wasn't even going to make it to the second iteration. I had to rethink things again.
Menger sponge attempt 4
After playing around with a lot of different sizes for the sponge, I tried with something much smaller as my basic unit:

And finally came up with something that worked.

It still seemed off to me; it looked like a poorly constructed house, but I was at least certain it was a Menger sponge. Not feeling fully satisfied with the final result of my sponge, I decided to try building another fractal pattern.
FRACTAL 2: The Sierpiński Triangle
I know Koch snowflakes are fractals, but they seemed too complex to be able to build with Legos. My thinking was that, Koch snowflakes have a faster rate of expansion, I think, for the surface area/size of the perimeter, so the likelihood was greater that I would run out of pieces before creating anything useful or wondrous... or even recognizable. Also, there are more points on a Koch snowflake, and making pointy things would be difficult. I was concerned, too, that the aspect of making it 3D presented more of a problem of construction.
However, I was starting to think that something similar to the Menger sponge, the Sierpiński Triangle (or Sieve) might work.
A Sierpiński triangle is constructed by taking a triangle (usually equilateral) and shrinking it in size by one half, then copying it two times, and placing the copies at with one point at each vertice of the base of the original triangle. At the second iteration, you repeat this process for each triangle, and so on through successive iterations.
I especially thought it would be a good candidate for construction considering that the Sierpiński Triangle doesn’t have to be composed of triangles, it can also be made up of other shapes, like squares! (The instructions above still work, more or less, just start with a square instead of a triangle. See example below.)
 .
.Sierpiński triangle attempt 1
I tried building one face, just to see if it would work, but I had hopes to build more.

This had definite promise.
I could easily extent this to 3D by making the face tilt in one direction

and then making subsequent faces connect top and bottom into a sort of hollow tetrahedron, and then I could stack four of them into a larger triangle. Worried I wouldn’t have enough pieces, I began to dig furiously into the Lego box.
Sierpiński triangle attempt 2
But in the end, it totally worked:


Then I realized that I am an idiot, and that I was completely wasting my time building something that looked like a Sierpiński Triangle, rather than building the thing itself. I mean, fractals are all about self-symmetry, and this thing I had built had the outer pattern on its surface, but my idea was to create 3D fractals, with my 3D materials.
Sierpiński triangle attempt 3
Beginning with a tiny pyramid of four 2x2 bricks, I began to build.



This is one iteration. From there, I build more.

Legos in the sizes and colors I needed were getting scarce. I wondered what my downstairs neighbors thought I was doing, as I scraped through my Lego bin over and over again. I had forgotten how much I loved that sound.
Eventually it came time for drastic measures, and I got to do something else I remember I secretly loved as a child -

Eventually, I found enough of everything I needed, and could finish the next iteration.

I went to sleep, fairly satisfied and having had a lot of fun.
But strange dreams plagued me, of my high school geometry teacher mocking me for my imprecision, and of every math test I was ever late or unprepared for... what could it mean?
When I awoke in the morning, I knew. I had made a grave error! Inspecting my fractal I realized it looked off, and the reason was because it was not entirely self-similar. I had made the layout of the base of the first iteration incorrectly, and it did not reflect my basic unit.
I was going to have to reconstruct the entire thing.
Sierpiński triangle attempt 4
After a lot of work, and a sad realization that I just did not have enough Legos to complete this differently constructed Sierpinski Triangle with the Legos I had and still maintain my easy to see color pattern, I was finally finished.

This is, indeed, a fractal. Though a bit unstable (I didn't have very many pieces of the correct size to try and connect some things differently in the second and third iterations so as to make it more stable) it holds its own.
Now, who wants to get together, bring their Legos, and build a really big one?5.
Other fun fractals
Oh! But, before I was done, when I was stewing over actual fractal Lego completion, while my backbrain was working on that problem, I also, created this dragon curve of Lego people heads:

I left a bloody trail of corpses in my wake

but here, you can better see their mathematically precise and smiling faces.
 .
. Ridiculous footnotes:
1 Wikipedia defines a fractal as "a rough or fragmented geometric shape that can be split into parts, each of which is (at least approximately) a reduced-size copy of the whole," who references The Fractal Geometry of Nature by Mandelbrot, B.B. (1982).
Another imprecise definition, but one that might be easier to grasp for those with some knowledge of the terms from calculus, is that a fractal is a curve that is everywhere continuous but nowhere differentiable.
2 The Cantor ternary set is defined as a perfect set that is nowhere dense (obviously analogous to the curvilinear definition I mentioned) and can be described mathematically as
(Cn-1)/3 U [2/3 + Cn-1)/3]
Also, does anyone know if LaTex or some equivalent works in praxes here? HTML math tags weren't working.
3 It only takes 20 2x2 bricks, rather than the 27 you might be thinking, intuitively (92) because one brick is removed from each face of the cube as well as the one at the very center. So the second iteration would be... only 400 bricks!
4 The Lego website was disappointing and a bit sad. When I was a kid it was my greatest dream, next to going to Antarctica, to work as a Lego designer someday. Legos today are not what they used to be. So many sets are comprised of fewer, larger, and more specialized pieces. I imagine it's harder for kids today to reconstruct them into something else other than what the instructions intend.
5 I am totally serious about this! We could keep our Legos separate (because who wants to lose any of their Legos?) by color coordinating, but it could totally be done. I am imagining a giant SF0 monument with pieces from all over! Collaborate with me!
my plan for a 9x9x9 cube of 2x2 bricks has a flaw...

Only using 2x2 bricks, there is no way of connecting the cube together!
unfinished and flat

but i ran into that same flatness problem (this one was unfinished before i discarded it, note how the space in the top is a not a square.)
base 3 with a green base

something was needed to hold this base together, though, at least at the outset.
not going to work.

yet again the 'square' is more of a rectangle. and a fuzzy one, at that. if i built the sponge this way - assuming i wouldn't run out of pieces - it would be incredibly squat.
clunky fractal.

the first completed Megner sponge is ugly. it also used too many pieces to possibly repeat it into further iterations.
it's working!

up through the base and first layer of 'cubes' this seems to be working. it needed flat pieces across the bottom to hold it together to start out with, though. i anticipated taking them off once successive layers were added and it increased in stability.
components

this was built entirely out of combinations of these pieces (not counting the flat ones on the bottom.) the corners turned out to be especially important.
the finished sponge

this one worked! and doesn't look that clunky. and it's out to... two iterations.
finished product sideways

this is the finished sponge, on its side. because the 1x1 pieces are *slightly* longer in height than either of their base dimensions, it is a bit rectangular after all.
two sides together

tilting them further made them quite unstable, but they should stabilize when all sides are connected
color coordinated three

this is out to three iterations. i've tried to keep colors whole and separate to make them easier to see.
second iteration again

it just looks really cool from this angle, like steps of some giant mayan temple or something.
top again!

still looks cool from above, but i ran out or temporarily misplaced some black pieces. (they were later found by my bed. i do some of my best thinking just before or during sleep.)
aesthetically corrected three

i replaced those unsightly grey pieces in the black second iteration once i found them.
a... four iteration - or five?

i am fuzzy on the way iterations are counted. do you count the outermost, largest triangle? (or from a construction from smaller pieces point of view, the basic pieces and the first base unit?)
anyway,

one night Mr. G took the flat Sierpiński triangle out to several more iterations than i got to, as i was forming a hollow tetrahedron with mine, when i could have been stacking them.
a last experiment

we also tried to build a more stable unit with this tetrahedral design as the base.
even more like a mayan temple than before

it was more stable, but used too many pieces to get very far.
Dragon curve of Lego Heads
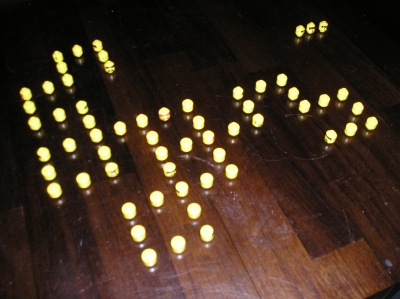
haha! the Lego nation has suffered for my art. i am a bloody legend to them now!
hand drawn examples of iterations
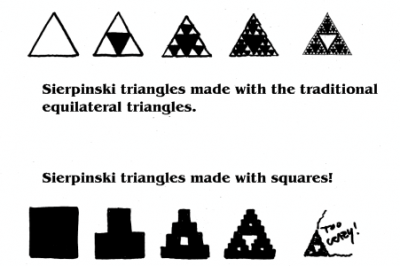
see how Sierpinski triangles can be constructed with other geometric shapes?
38 vote(s)
- GYØ Ben
- help im a bear
- Lincøln
- Not Here No More
- Tøm
- auntie matter
- a actinism torrents joins
- JJason Recognition
- teh Lolbrarian
- Mr. O.
- teucer
- Jellybean of Thark
- Burn Unit
- Evil Sugar
- Rainy
- Julian Muffinbot
- Loki
- anna one
- JK Bobbins
- Flitworth
- Ayma Mack
- Sparrows Fall
- Haberley Mead
- susy derkins
- zer0gee
- Dela Dejavoo
- rongo rongo
- LittleMonk
- Darkaardvark
- The Alienator
- Ben Whitehouse
- Edwin Farnham Butler III
- HFXØ Sponty
- Rachel's Reflection
- Spidere
- JTony Loves Brains
- rehsamsevoL Lovesmasher
- MsGoblinPants Extraordinaire
Favorite of:
Terms
shplank, foecake, foecakefleur11 comment(s)
So many sets are comprised of fewer, larger, and more specialized pieces. I imagine it's harder for kids today to reconstruct them into something else other than what the instructions intend.
yes, this is really sad. like playgrounds getting so "safe" that there is nothing for kids to do on them anymore except sort of run around on platforms with high railings and go down weeny slides.
The gummies would like to live in a fractal pyramid. They will attempt to acquire the necessary building materials.
Note that just as a square can be used as the building block of a Sierpinski gasket, so can a gummy.
Just a thought.
True. However, getting the gummies to hold still long enough to complete the entire construction may prove difficult -- they get bored easily, and have a tendency to wander off.
There would need to be glue involved, also, or the whole thing would collapse.
I *just* now thought of a way I could create the Koch snowflake curve fractal. Or two ways, possibly. Curses!
...I will work on this tonight, and if anything pans out, update immediately.
My favorite: The fractal of DEATH!

Do you think if you zoom in, you would find that each corpse is constructed of piles of corpses?
I do.
I liked how you kept trying different approaches with the lego.
So, I've been out of town, and also had a houseguest, so I haven't been able to test out the Koch snowflake patterns, which I still intend to do because I have a feeling they will be very pretty.
But I was thinking of it today, and looking at SF0, and noticed this.
I've been Art Burgled! Ach, me Legos!
It looks like I'll have to get my Legos back before I can test out that Koch pattern....






























































I love the quotes when you roll your pointer over the pictures!