Discovering What Doesn't Change by Markov Walker
December 15th, 2009 9:52 PM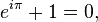
In the pdf I've included I go into what this means and why it's true. But for this brief text introduction, I'll talk about my favorite constant in the identity, Euler's constant, e. Most of the information here and in the pdf is drawn from Wikipedia's entries on Euler's Identity and Taylor Series, a math question corner at the University of Toronto, and the math page's calculus introduction to logarithms and exponents.
Update: I've found two excellent posts at http://betterexplained.com/ that give a really good analogy to help guide your understanding of both e and Euler's formula. First you should try to understand e as the amount of money you have if you start with $1 and wait 1 unit of time at 100% interest compounded continuously. Then you should understand e^(x*i) as the location you'd be at in the complex plane after rotating x radians around the unit circle. Thanks to Dan for brining this article to my attention.
Pi gets a great deal of attention, but e is really the king of mathematical constants. Sure, some people famously memorize pi out to thousands of decimal places, and nobody does this for e. I blame marketing; pi is the ratio of a circle's circumference to its diameter. That's simple to understand. e is requires calculus to appreciate, which makes its appeal less broad.
e is a transcendental number, meaning cannot be represented as a ratio of integers, nor as a rational root of any rational number. It is approximately 2.71828182845904523536 to twenty decimal places. It was first discovered when Jacob Bernouli was working on compounding interest and discovered that

converges to a finite constant, e.
The calculus page motivates a definition of e based on the derivatives of exponential functions. If you don't know calculus, the derivative of a function tells you how that function is changing locally at some particular point. For example, if I give you a function that takes a time as an argument and gives you the position of some object at that time, the derivative of that function with respect to time gives a function that takes a time and gives the speed of the object at that time, the speed being the local change in the position of the object. The derivative of this speed function gives a function from times to the acceleration of the object, the acceleration being the local change in speed.
Euler's constant has the remarkable property that
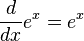
Thus, e^x is its own derivative. It is the only function that is equal to its derivative. For all a, the derivative of a^x = k*(a^x) for some k. e is the unique value for a for which k=1.
e can also be represented as an infinite sum:
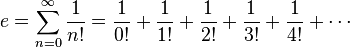 .
.Better Explained provides a good way to think about this infinite sum. Suppose you have $1 accruing 100% interest for 1 year. The first term is your principle. The second term is the amount your principle will earn you in a year. The third term is the amount that second term will earn as it gets compounded continuously. The fourth term is the amount of interest earned compounded from the third term. And so on, such that each term is the interest earned on the money in the term before it.
e is the global maximum of the function

And finally, e is the expected value of U,

with X drawn from the uniform distribution on the interval (0, 1).
Update: Daniel Wedge puts it all together in a wonderful song.
15 vote(s)

Sass Afrass
5
Juliette
5
Spidere
5
gh◌st ᵰⱥ₥ing
5
Dan |ØwO|
5
Waldo Cheerio
5
Joe
5
Picø ҉ ØwO
5
Pixie
5
Samantha Ebay |ØwO|
5
done
5
[øwo] lady minirex
5
Likes Music 0w0
5
Idøntity matrix
5
Cookie
Favorite of:
Terms
learning, math, beauty, mathematics, science8 comment(s)
Actually, the algorthim you just described is the final description of e in this proof, the expected value of U.
holy crap that is SO COOL and it worked-ish with my small sample size (24) e = ca. 2.75.
Math is awesome.
I'm curious what the distribution of U is. I expect the median and mode are three, with the tail dropping off rather fast.
This proof has been flagged by 15 of your fellow players (for the benefit of all, flags are anonymous). As such, it has been automatically disapproved. Most likely, they've posted comments explaining why they're displeased. If you think you may be the victim of a bug, injustice, or a gang of Rubins, hit up the contact page.
If you think you can fix this proof, click 'edit this completed task', then 'Un-Submit Proof' (at the bottom of the editing page). Make your changes, hit Submit again, and the flags on this proof will be cleared.
My favourite expression of growth is the Fibonacci sequence. Wether concious or not craftsmen have used the proportions throughout history to produce aesthetics. My favourite application was on some of the finest medieval swords.
This little youtube film explained e to a layman, like myself:
http://www.youtube.com/watch?v=yTfHn9Aj7UM&feature=player_embedded
It pleased me to find out that the fibonacci sequence and e are aspects of the same thing. 5 points for you! And I don't think this should have been flagged. I vote to unflag it :-)
Cookies to you!












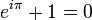







Another way to find e:
1. Take random decimals until they add up to or are greater than 1.
2. Count how many random decimals it took (let's call this number n).
3. Do this over and over, averaging n each time. It takes time, but this turns out to be e!
I love e. My favorite thing is probably that the tangent line at (0,1) has slope of 1. That is gorgeous.